前一章详解了傅里叶变换中信号非相干性导致的频谱泄漏问题,分析不同窗函数(如Hamming、FlatTop等)对频谱精度和分辨率的影响,并给出窗函数选择的实用建议。
【前文回顾】德思特干货 | AD/DA动态分析中的信号窗口处理技术
本章将继续介绍ADC直方图测试:
一、简介
A/D 转换器的线性度计算以转换点为基础。对转换器的输入施加精确的斜坡信号是进行静态分析的一种方法。转换点(或跳变点)计算算法需已知准确的输入电压。直方图(或码密度)法是 ADC 测试的另一种常用技术。有两种常用的直方图方法:线性斜坡法和正弦波法。
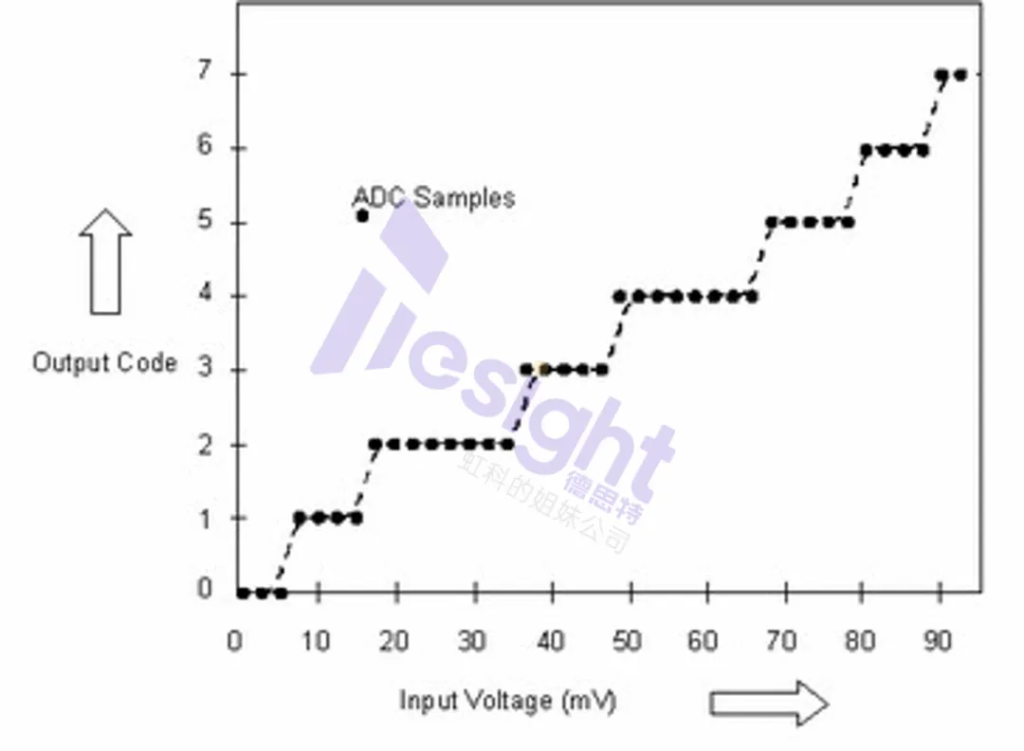
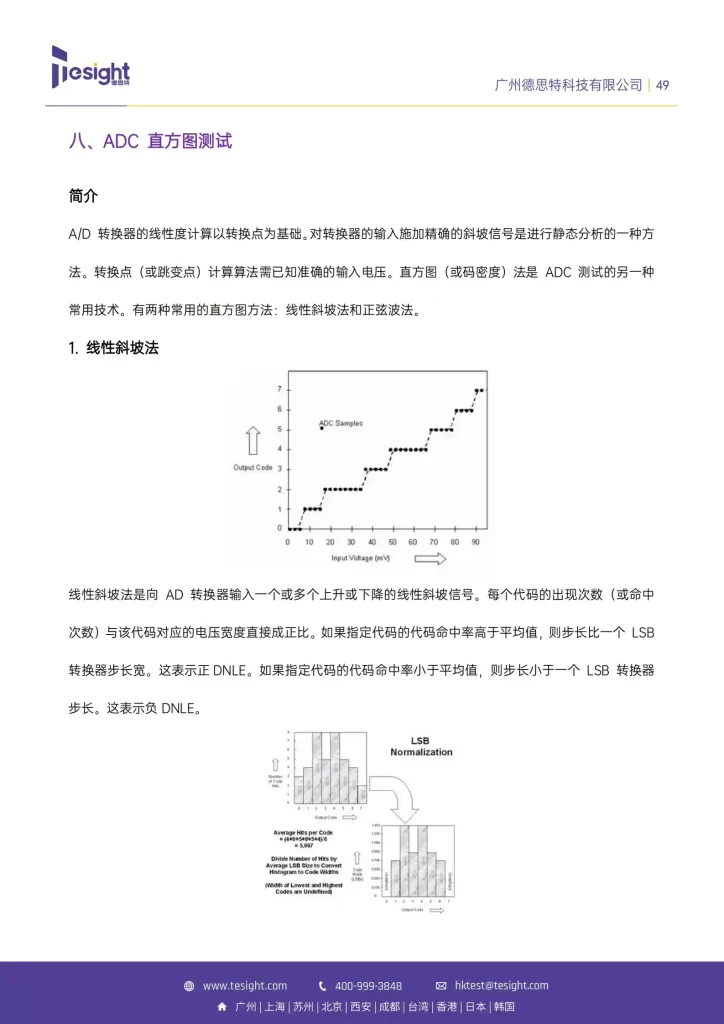
二、线性斜坡法
线性斜坡法是向 AD 转换器输入一个或多个上升或下降的线性斜坡信号。每个代码的出现次数(或命中次数)与该代码对应的电压宽度直接成正比。如果指定代码的代码命中率高于平均值,则步长比一个 LSB 转换器步长宽。这表示正DNLE。如果指定代码的代码命中率小于平均值,则步长小于一个 LSB 转换器步长。这表示负DNLE。
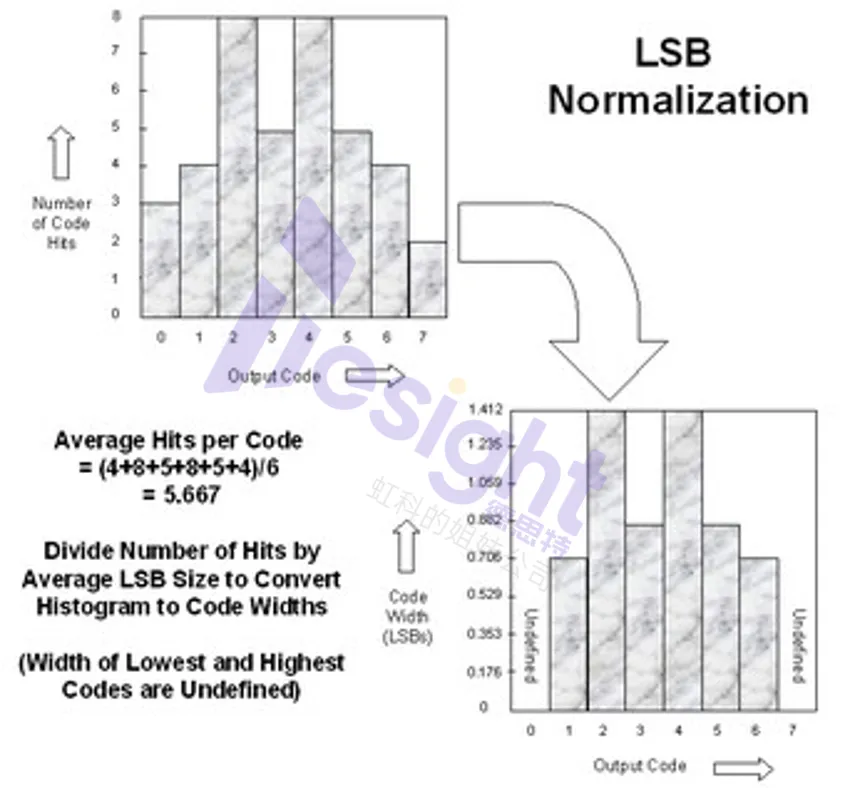
代码 0 和最后一个代码没有意义。这两个代码的代码出现次数可能更少,也可能更多,因此这些代码宽度是未定义的。在线性斜坡直方图计算中,这两个代码的出现次数将被忽略。
由于每个代码的出现代表每个步长的 DNLE,因此将这些 DNL 误差相加将得到一条 INLE 曲线。
每个代码的应用步数决定了测量分辨率。例如,如果每个 ADC 代码的步数为 10(如 8 位转换器为 2560 步),则测量分辨率为 1/10 LSB。
三、正弦波法
正弦波法将一个或多个周期的正弦波信号应用到 AD 转换器的输入端。
正弦直方图测试与线性斜坡测试之间存在一些差异:
- 通常,产生纯正的正弦波比产生精确的线性斜坡更容易。
- 线性测试是静态性能测试,正弦测试是动态性能测试。
- 线性测试的电压分布均匀,正弦波的电压分布不均匀。正弦波在接近低电压和高电压时有更多的电压阶跃。
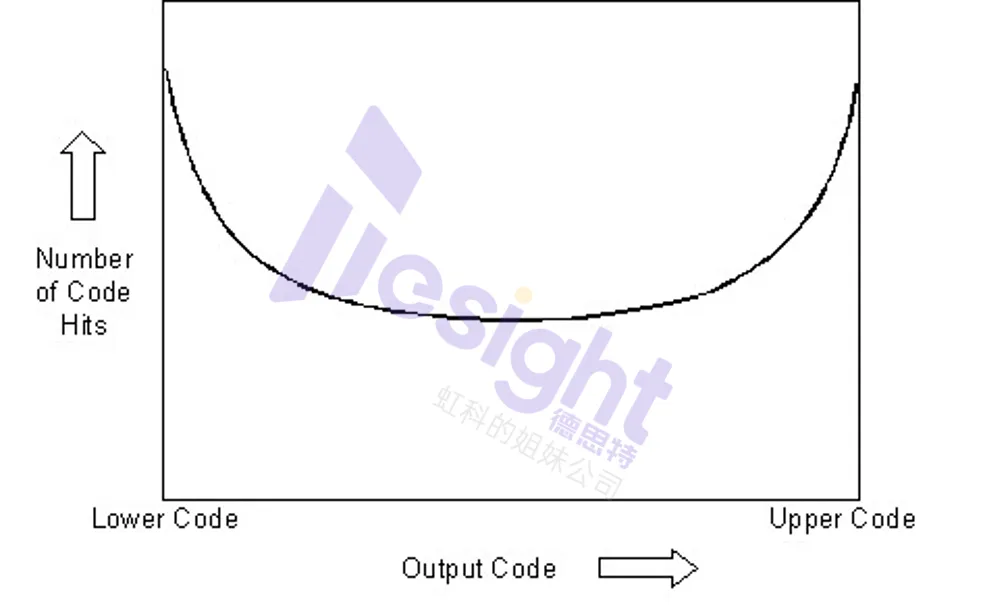
必须对正弦波测试中电压分布不均的情况进行补偿,以重新构建每个编码的理想编码发生率。要进行这一归一化处理,必须知道信号的偏移和振幅。直方图中上下层代码的命中数可用来计算输入信号的偏移和振幅。
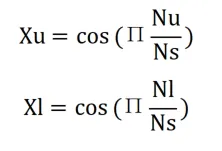
Nu 是上层代码被击中的次数,Nl 是下层代码被击中的次数,Ns 是样本数(代码出现的总和),N 是转换器的分辨率(以比特为单位)。
一旦知道偏移和振幅,就可以计算出代码命中的理想分布。
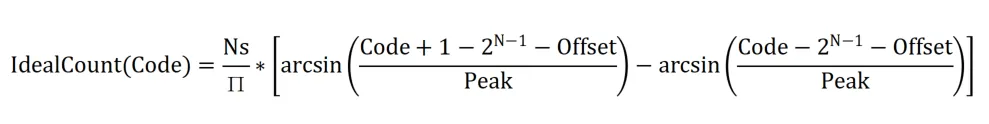
以下公式可用于确定达到所需测量分辨率时输入信号所需的激励步数:
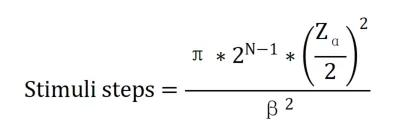
其中,N 代表 ADC 位数,Zα/2 代表置信度,β 代表以 LSB 为单位的 DNLE 分辨率。
示例:10 位 ADC,所需的 DNLE 测量分辨率 (β)为 0.1 LSB,置信度为 95% (Zα/2):
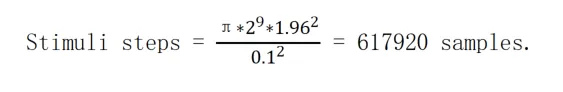
置信水平(Zα/2)的常用值为
90% : 1.645
95% : 1.96
99% : 2.576
激励步长计算器

如有需要可联系德思特获取工具链接
德思特ADC测试平台特点
✓ 完全集成的ADC测试解决方案
✓ 采样频率高达200/400 MHz
✓ 无与伦比的信号发生质量和精度
✓ 支持所有线性/动态测试
✓ 灵活和通用的数字IO
✓ 扩展分析软件ATView\WaveAnalyzer
✓ 静态、直方图测试
✓ 易于用户自定义的测试脚本
- 相关产品

• 德思特ADC/DAC自动化测试系统
德思特ADC/DAC测试系统是一套9槽ATE芯片测试平台,模块化设计确保灵活性与扩展性,专注于数模及模数转换芯片的深度测试。系统囊括ADC/DAC全范围线性动态评估,搭载DIO时钟同步模块,可测8-24 bit ADC/DAC,以高达400 MHz的采样速率,重塑高效芯片测试新标准。



德思特ADC、DAC芯片测试白皮书
- 精准术语解释:20+关键ADC术语全解析,全面理解采样、抖动、非线性误差等影响性能的核心因素。
- 全流程参数计算:静态参数、动态分析、ENOB / SNR / SFDR / THD等核心指标计算方法详尽剖析。
- 实例操作指导:涵盖AD7671 / AD9244 / LTC2641等多种芯片真实测试配置与操作流程指导。
