德思特干货 | AD/DA 动态分析中的信号窗口处理技术

前一章详解了TX7006上的线性计算，AD/DA动态分析中的傅里叶变换和动态参数计算。

【前文回顾】德思特干货 | ATX7006线性计算与AD/DA动态分析解析

本章将继续介绍AD/DA动态分析中的信号窗口：

一、简介

傅里叶变换假定（采样）信号是无限的。因此，最后一个采样点的幅度应恰好在第一个采样点（的幅度）前一个采样点结束。采集到的正弦波数量应为整数。换句话说，如果将采集到的信号依次重复排列，信号应是连续的。具有整数个采样点的采集信号是相干的。

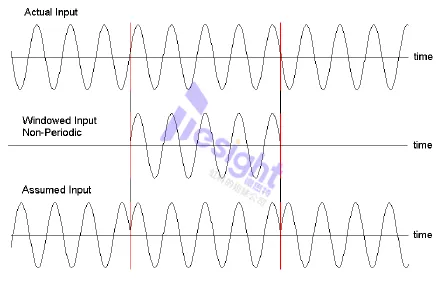
并不总是能够捕捉到整数的正弦波（也就是2的幂次）。对于傅立叶变换来说，这意味着信号是不连续的（信号的终点和起点不平滑）。在频谱中，这将导致频谱泄漏。见下图：按下“显示频谱”按钮，在相干和非相干之间切换。

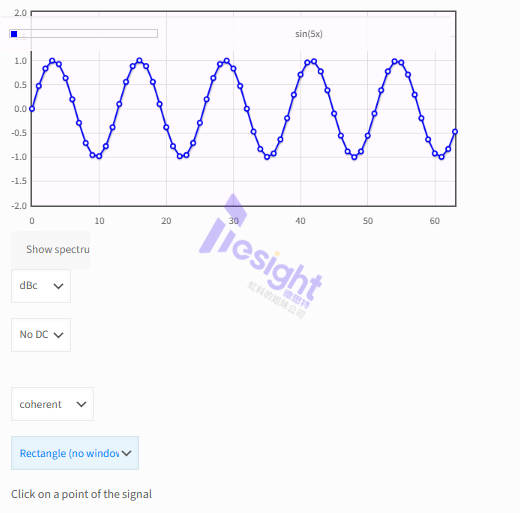
二、不连贯信号的窗口处理

对不连贯的捕获信号进行傅立叶分析，将无法计算出可用的参数（SINAD、信噪比等），而且谐波可能会在频谱中被忽略。为了减少不连续性的影响，我们可以在信号开始和结束时减小捕获信号的振幅。这正是信号窗口的作用。在上图中显示信号并选择一个窗口。在频谱中，它会在感兴趣的频点周围产生额外的频点。信号窗口的计算公式位于绘图下方。该信号与捕捉到的信号相乘。

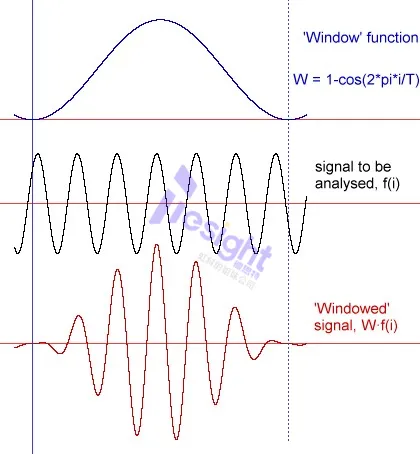
1.幅度误差

在上图中选择相干、矩形窗口，以电压峰值显示频谱。振幅正好与1Vpeak吻合。现在选择非相干，注意振幅误差。载波的能量分散到了其他频带。选择dBc（相对于载波的dBs）时，可以更好地看到这一点。切换回Vpeak，选择相干信号、扫描窗口。载波振幅为0.5V。其他能量被置于载波两侧的2个分区中。总振幅为1Vpeak（0.5V+2*0.25V）。然后选择非相干信号。仍然会有振幅误差，但会小于矩形窗口。

2.参数计算

正如我们在前面的示例中看到的，信号窗口可以减少频谱泄漏，并将信号能量置于信号周围的额外分段中。参数计算将更加合理，谐波也能在频谱中重新识别。RifeVincent4窗口会将感兴趣信号的几乎所有能量都置于信号周围的额外频带中。然而，这其中存在一个问题。为了说明这一点，请参阅下一个实验。

3.窗口频率分辨率问题

显示频谱（按下“显示信号”按钮），选择dBc、0.5V直流、相干信号并选择Hamming 窗。信号能量分布在3个bin中，即5号bin及5号bin两侧各1个额外bin。直流能量分布在第1和第2个bin中，信号与直流bin之间的bin（2号和3号bin）为噪声bin。

选择RifeVincent4窗。信号能量分布在9个bin中（去除直流后计数），中心位于5号bin位置，5号bin两侧各有4个bin。直流分量的情况同理。由于信号与直流bin之间仅有3个bin，因此1号至4号bin中同时包含直流和信号成分。

谐波bin与噪声bin之间也可能发生同样的情况。如果某谐波bin的幅度低于或等于其周围噪声bin的幅度，该谐波会“吸收”（泄漏）噪声bin的能量。因此，当启用窗函数且谐波幅度等于或低于噪声时，总谐波失真（THD）可能显著恶化。

三、选择窗函数

窗函数之间的一个重要区别在于主瓣宽度和旁瓣特性。主瓣由中心频率及其两侧的一个或多个频率bins（频段）组成。当选择相干信号（无直流）时，这一点可在上述绘图中观察到。更改窗函数将改变中心频率周围的bins数量。旁瓣是不属于主瓣的bins。主瓣宽度决定了频率分辨率（即我们区分信号的能力）——主瓣越宽，频率分辨率越差，但幅度精度越好。如果幅度精度是关键问题，FlatTop 或 Blackman-Harris 窗可能是不错的选择，但其主瓣较宽，导致频率分辨率较差。

Hamming 窗和 Hanning 窗的形状相似（也可参见两者的数学表达式）。它们的幅度精度较差，但频率分辨率优于 FlatTop 和 Blackman-Harris 窗。两者的主要区别在于旁瓣的滚降速率。

RifeVincent4 窗的旁瓣电平极低，但主瓣较宽。对于单音信号下的A/D和D/A转换器动态测试，这可能是一个合适的选择。但需注意，由于主瓣较宽，谐波的主瓣也会较宽，导致相邻噪声bins的能量泄漏到谐波bins中，这通常会导致总谐波失真（THD）较差（相对而言）。

1.窗函数特性

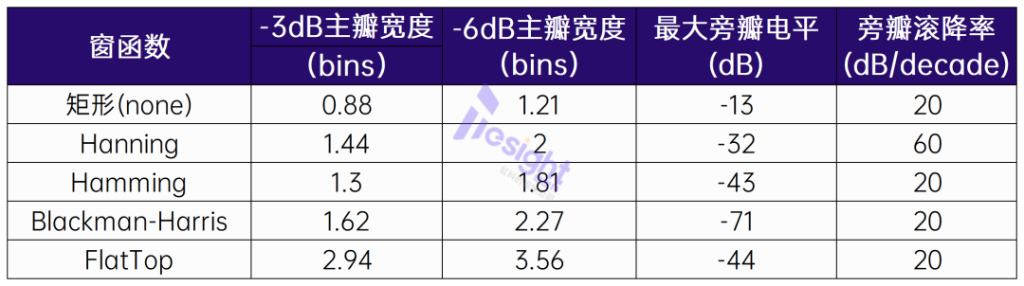
下表列出了各种窗函数的一些特性。最大旁瓣电平是指相对于主瓣而言，最大旁瓣的电平值（以分贝为单位）。旁瓣滚降速率是指旁瓣峰值随频率每十倍频程衰减的速率（以分贝/十倍频程为单位）。